Optimal Congressional Redistricting and Gerrymandering

One of the first classes I took at UT Austin was a linear optimization course. As a final project, a classmate (Tiffany Tillett) and I decided to apply the course to eliminate gerrymandering. Hopefully someone at the state legislature takes a look at this prior to redrawing the congressional maps following the 2020 census. Here’s a quick report of what we found. To view the full report, presentation, and our code, please checkout this github repo.

Utilizing Linear Programming to Eliminate Gerrymandering

Background

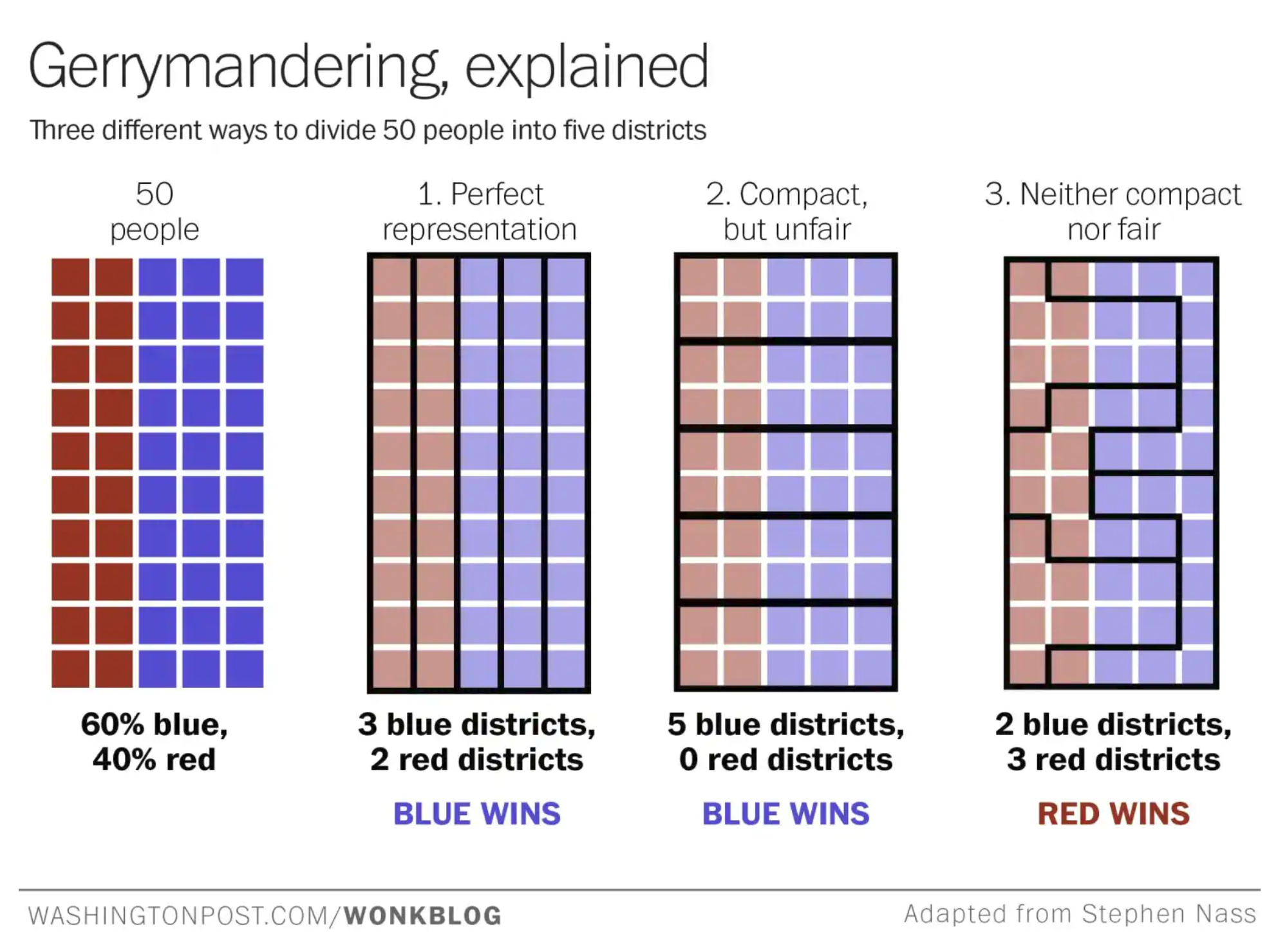
Gerrymandering is the process of manipulating the boundaries of political districts to favor a particular party. When this occurs, there are cases where the majority of the population may vote with one party but the majority of the seats are with the other party. This should not occur.

This project was a proof of concept using the state of Rhode Island to see whether linear programming could be used to draw legal, fair political districts without human influence to avoid the occurrence of the above mentioned scenario

Criteria

There are certain criteria to identify whether or not the political districting was done well. Some of those criteria are:

1. Integrity: Each territory must belong to exactly one district
2. Contiguity: All areas covered by a single district must be connected somehow
3. No enclaves: A single district should not surround another district.
4. Compactness: A district should not be unnecessarily spread out or odd shaped
5. Population equality: districts should contain a similar number of constituents

From these criteria, we can see that this is really an optimization problem. We want to form some assignment of census blocks to districts that satisfies the first three requirements and finds a good balance between compactness and population equality. We could also factor in whether the districts have balanced proportions of different ethnic groups and political preferences. Since this does boil down to an optimization problem, linear programming is the perfect tool to tackle this.

First Attempt

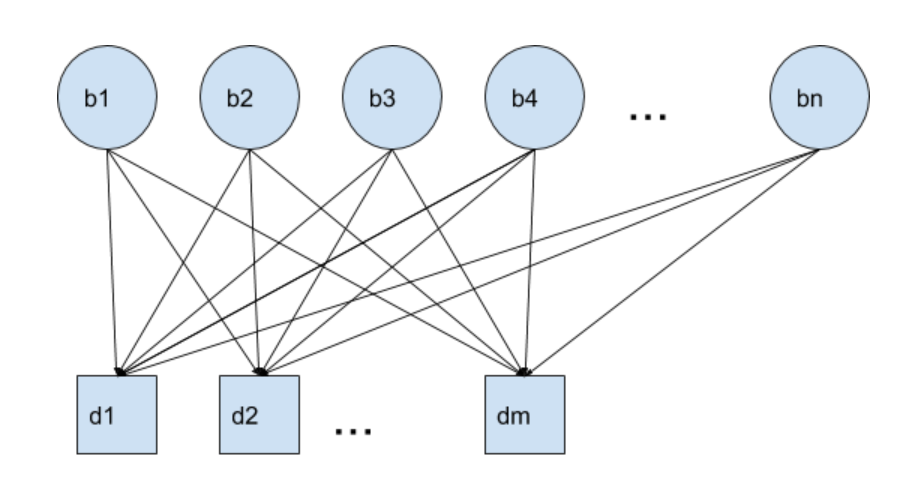
In order to accomplish this, we first wrote constraints to cover integrity and wrote an objective function which covered compactness and population equality. At this stage, we did not explicitly cover enclaves or contiguity, hoping that compactness would indirectly satisfy these criteria. We used a network flow formulation to accomplish this where each “block” has an arc to each district center.

Variables:

1. F : where F_ij is the number of people from block i assigned to district j
2. X: a binary variable where X_ij is 1 if block i is assigned to district j and 0 otherwise
3. s: the population of the smallest district
4. l: the population of the largest district
5. g: the gap in size between the largest and smallest districts

Parameters

1. d_ij is the distance from block i to the center of district j. The district centers were calculated by solving another optimization problem to minimize the population weighted squared distances between electoral districts and meshblocks based on the current district assignments.
2. p_i is the population of block i
3. c_d is the component of the cost vector associated with compactness
4. c_p is the component of the cost vector associated with population equality

Objective Function

minimize: c_d∑_ij (d_ij p_i) + c_pg

Constraints

1. All people in the district must be assigned to a district
   ∑_j F_ij = p_i for all i

2. X must be 1 if the population flow is > 0. X is 0 otherwise
   F_ij <= data-preserve-html-node="true" M * X_ij for all i,j and some large M

3. Find the smallest district population
   s <= data-preserve-html-node="true" ∑_i F_ij for all j

4. Find the largest district population
   l >= ∑_i F_ij for all j
5. g = l - s

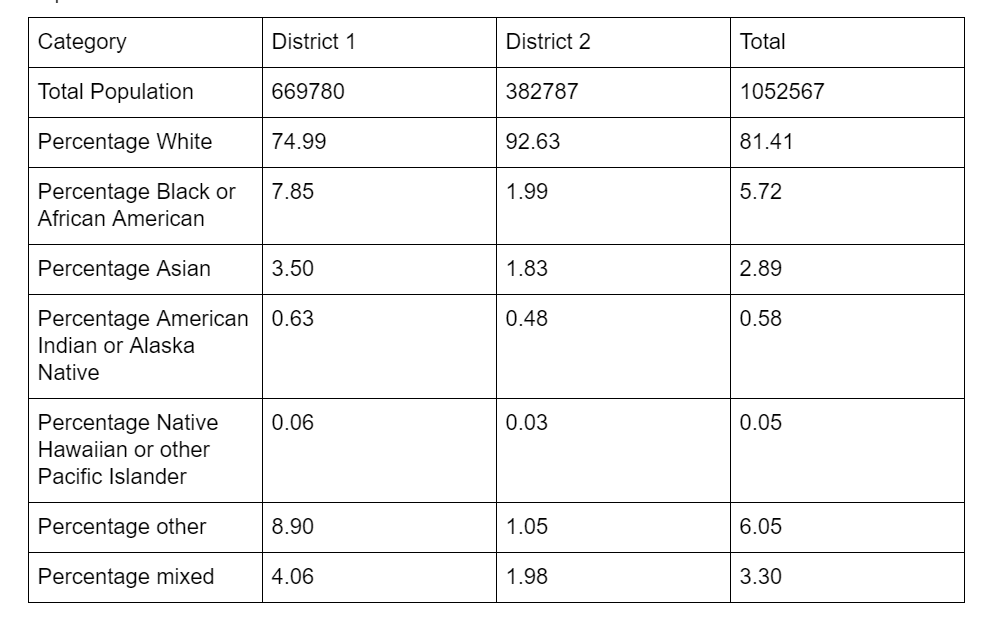
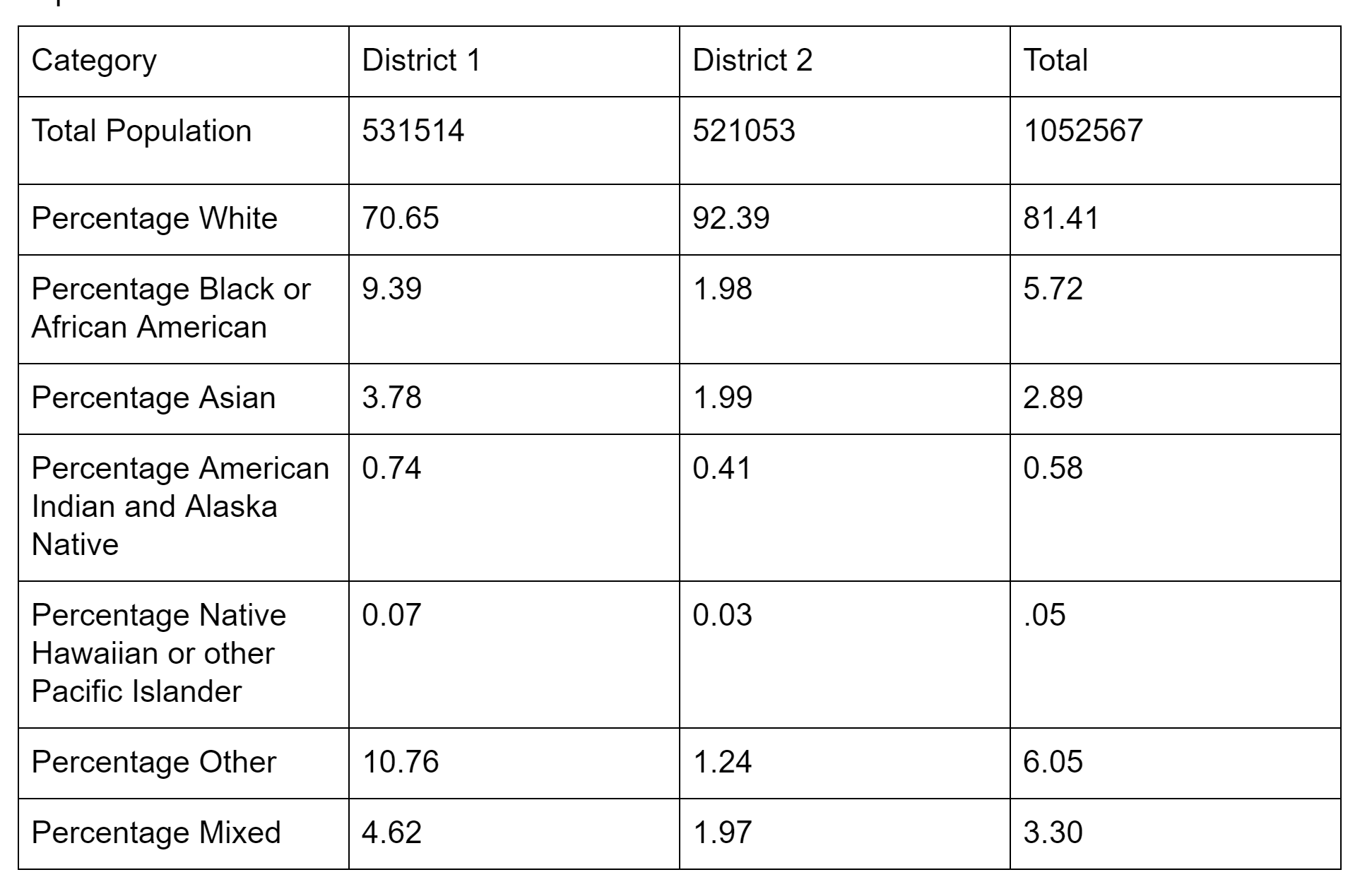
Population Results

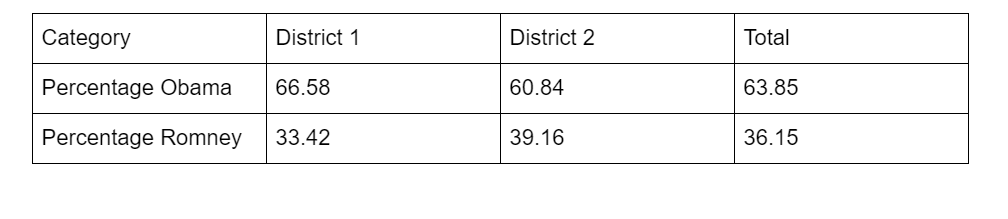
Political Results

Based on 2012 presidential election results

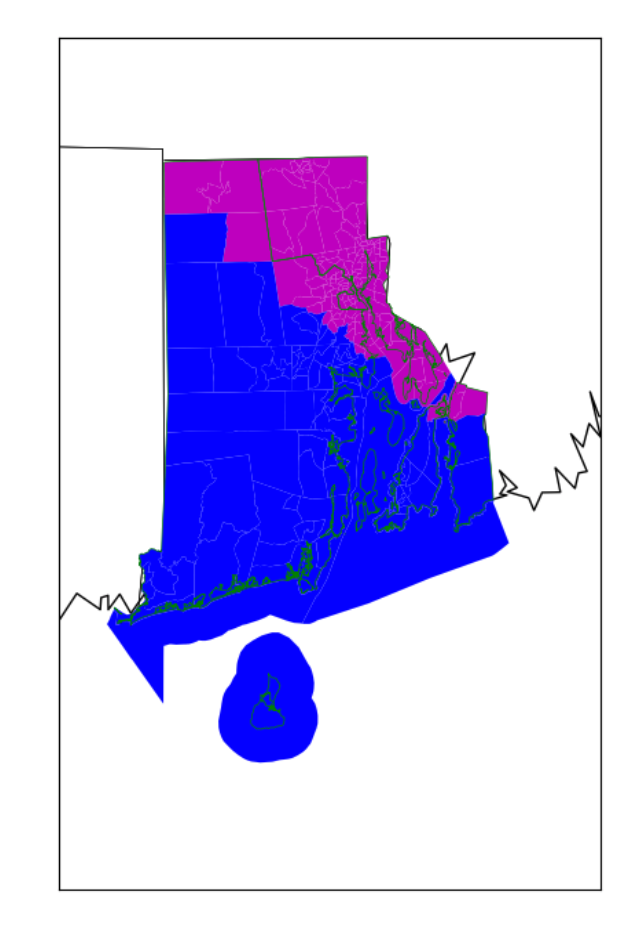
Resulting Map

We can see that there is some mixing of the blue and magenta which violates the contiguity requirement. We can also see that the population results are not quite balanced. Let’s revise our formulation to include constraints that resolve this and also achieve better population equity.

Second Attempt

Additional Variables

We will first introduce some additional variables:

1. y: where y_ijk indicates the amount of flow from block i to block j for district k
2. w: where w_ik is 1 if block i is the hub for district k and 0 otherwise Note: a block i can be considered a hub of district j if block i can be reached by all other blocks in district j

Additional parameters

And some additional parameters:

1. p: the target population of each district which in this case is simply the total population divided by the number of districts
2. n: the total number of blocks
3. 𝛼: tolerance on each district's population deviation from p

Additional Constraints

Now we can add our contiguity constraints and population constraints

1. Each district must have exactly one hub
   ∑_i w_ik = 1 for all k
2. Flow constraint: flow into block i cannot be greater than the total number of blocks
   ∑_j y_jik <= data-preserve-html-node="true" (n - 1) X_ik for all k,i and for all j in neighbors[i]
3. Lower bound on district population
   ∑_i p_i * X_ik >= (1 - 𝛼) p for all k
4. Upper bound on district population
   ∑_i (p_i * X_ik <= data-preserve-html-node="true" (1 + 𝛼) p for all k

Population Results

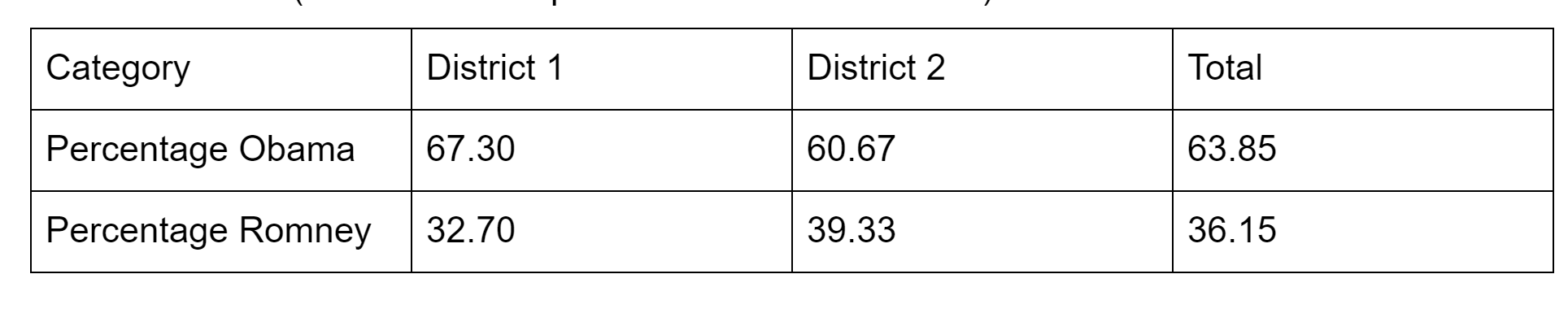
Political Results

Based on 2012 presidential election results

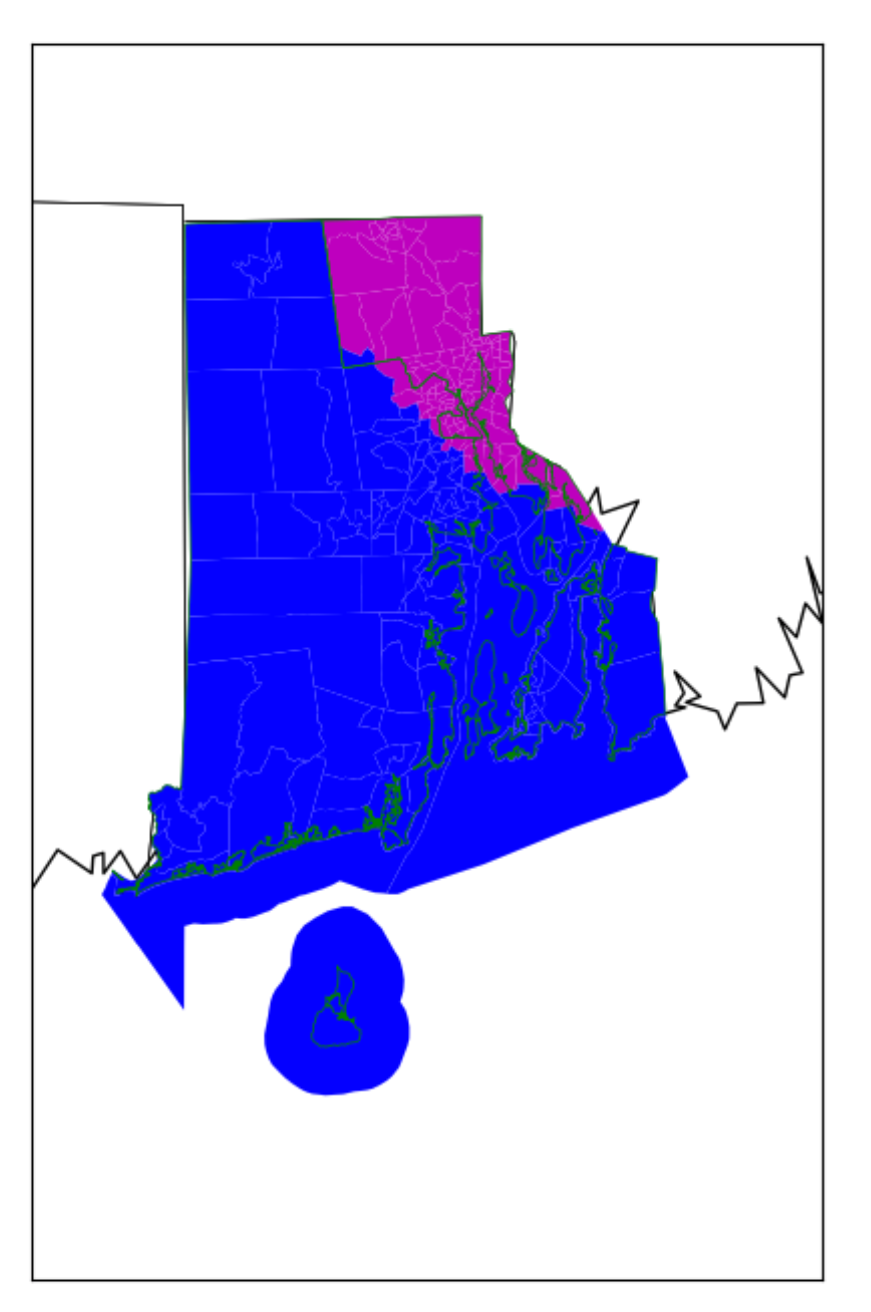
Resulting Map

We can see that there is no longer any mixing of the blue and the magenta. In addition, we have overlaid the lines of the current district boundaries (green). We can see that the current version has some oddly drawn lines which are an indication of gerrymandering. This is eliminated in our updated version.

Comparison to Current Districting

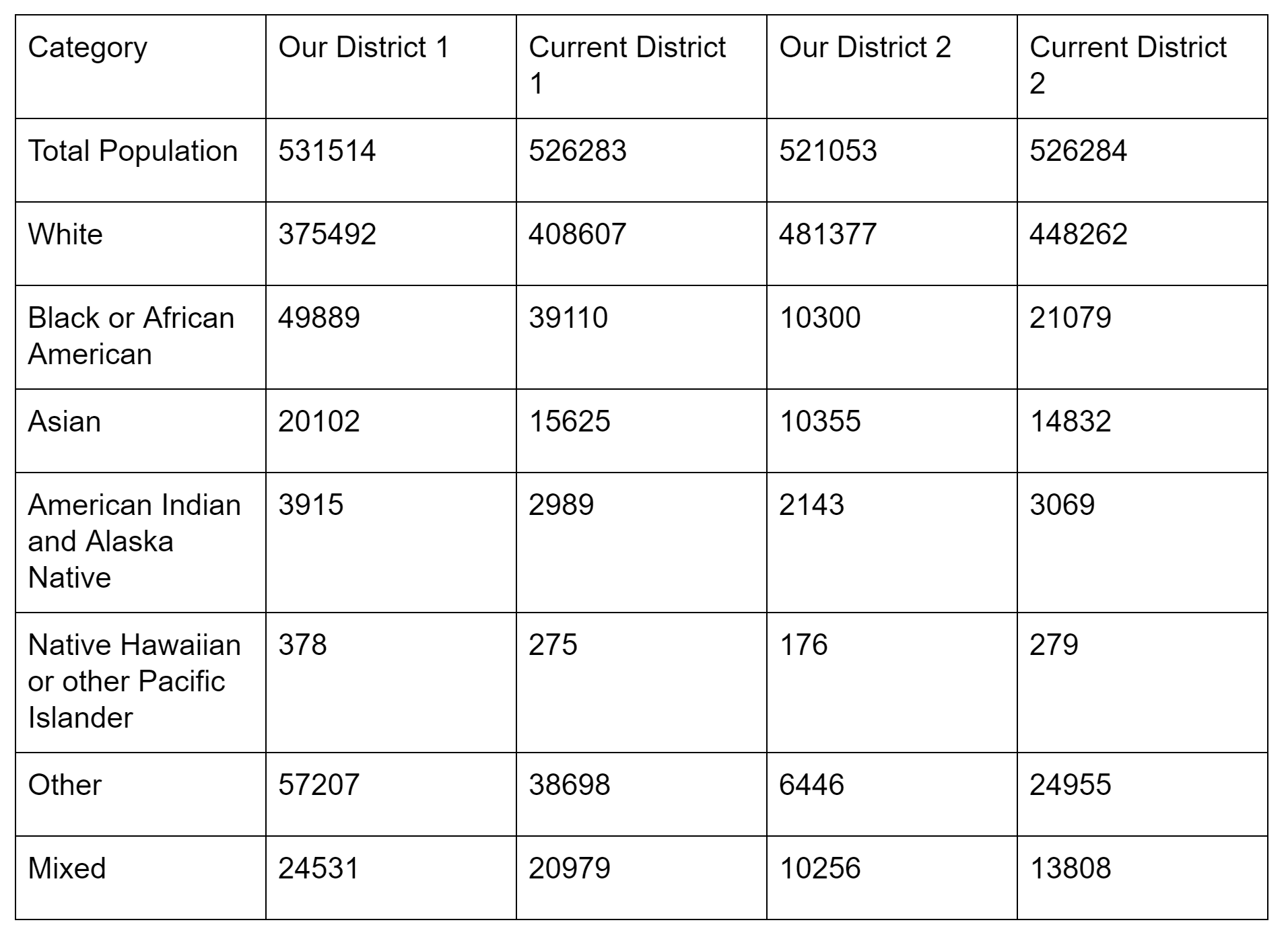
Our districts are not as population balanced or racially balanced as the original ones, but as seen above, they are more compact. We could improve our formulations by reducing the value of alpha, by using census blocks instead of census tracts for more flexibility and by incorporating race balancing into the formulation

Conclusions

Linear Programming is a promising way to generate political districts without human intervention. We were able to successfully generate population balanced, contiguous, compact districts. These districts are also fairly balanced politically. However, we could spend some time characterizing the cost function to potentially get even better results. In addition, our model does not incorporate race or political balancing at all.

One challenge with this approach is that it is very computation heavy. It is preferable to use smaller chunks when assigning districting to get more flexibility and make it easier to balance the population, but even the small state of Rhode Island has a very large number of census blocks (~25000). The initial formulation did not have as many constraints or variables, so the problem size was still manageable. However, the second formulation caused the size to increase to the point that we were unable to solve it on our laptops, so we had to allocate census tracts instead of census blocks. The results of the first formulation which are reported here were calculated using census tracts so that we could do an apples to apples comparison of both versions.

References

• Institute for Geoinformation and Cartography, Vienna University of Technology, GuÞhausstrasse 27 ^ 29, Vienna 1040, Austria; e-mail: shirabe@geoinfo.tuwien.ac.at Received 28 September 2007; in revised form 6 August 2008; published online 2 October 2009

• Scozzari, Andrea. “Districting and Gerrymandering.” 8-12 July 2014. University Niccolo Cusano. http://research.illc.uva.nl/COST-IC1205/documents/Caen-2014-Slides/Scozarri.pdf

• George, John A and Bruce W Lamar and Chris A Wallace. “Political district determination using large-scale network optimization.” Socio-Economic Planning Sciences. March 1997. Science Direct